 \n",
"___"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Principal Component Analysis\n",
"\n",
"Let's discuss PCA! Since this isn't exactly a full machine learning algorithm, but instead an unsupervised learning algorithm, we will just have a lecture on this topic, but no full machine learning project (although we will walk through the cancer set with PCA).\n",
"\n",
"## PCA Review\n",
"\n",
"Make sure to watch the video lecture and theory presentation for a full overview of PCA! \n",
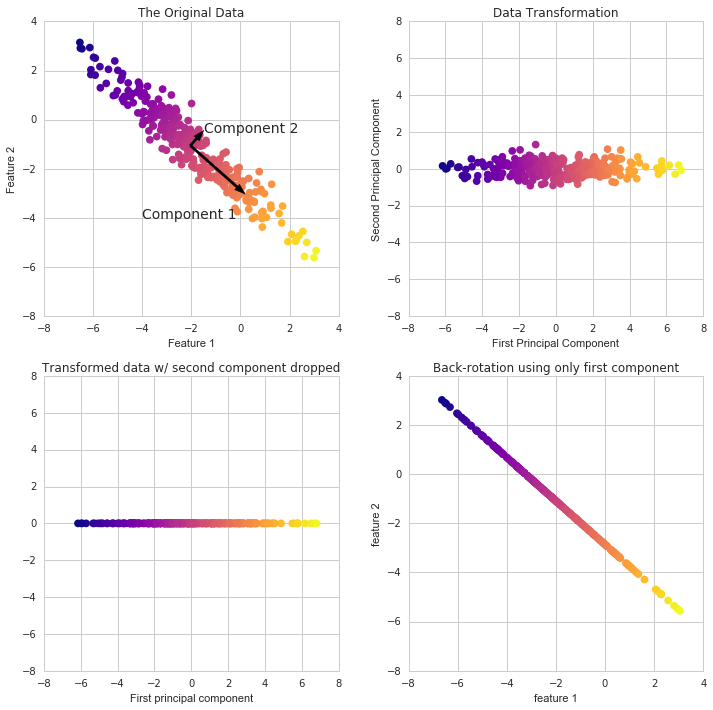
"Remember that PCA is just a transformation of your data and attempts to find out what features explain the most variance in your data. For example:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"
\n",
"___"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Principal Component Analysis\n",
"\n",
"Let's discuss PCA! Since this isn't exactly a full machine learning algorithm, but instead an unsupervised learning algorithm, we will just have a lecture on this topic, but no full machine learning project (although we will walk through the cancer set with PCA).\n",
"\n",
"## PCA Review\n",
"\n",
"Make sure to watch the video lecture and theory presentation for a full overview of PCA! \n",
"Remember that PCA is just a transformation of your data and attempts to find out what features explain the most variance in your data. For example:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Libraries"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import pandas as pd\n",
"import numpy as np\n",
"import seaborn as sns\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The Data\n",
"\n",
"Let's work with the cancer data set again since it had so many features."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn.datasets import load_breast_cancer"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cancer = load_breast_cancer()"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"dict_keys(['DESCR', 'data', 'feature_names', 'target_names', 'target'])"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cancer.keys()"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Breast Cancer Wisconsin (Diagnostic) Database\n",
"\n",
"Notes\n",
"-----\n",
"Data Set Characteristics:\n",
" :Number of Instances: 569\n",
"\n",
" :Number of Attributes: 30 numeric, predictive attributes and the class\n",
"\n",
" :Attribute Information:\n",
" - radius (mean of distances from center to points on the perimeter)\n",
" - texture (standard deviation of gray-scale values)\n",
" - perimeter\n",
" - area\n",
" - smoothness (local variation in radius lengths)\n",
" - compactness (perimeter^2 / area - 1.0)\n",
" - concavity (severity of concave portions of the contour)\n",
" - concave points (number of concave portions of the contour)\n",
" - symmetry \n",
" - fractal dimension (\"coastline approximation\" - 1)\n",
" \n",
" The mean, standard error, and \"worst\" or largest (mean of the three\n",
" largest values) of these features were computed for each image,\n",
" resulting in 30 features. For instance, field 3 is Mean Radius, field\n",
" 13 is Radius SE, field 23 is Worst Radius.\n",
" \n",
" - class:\n",
" - WDBC-Malignant\n",
" - WDBC-Benign\n",
"\n",
" :Summary Statistics:\n",
"\n",
" ===================================== ======= ========\n",
" Min Max\n",
" ===================================== ======= ========\n",
" radius (mean): 6.981 28.11\n",
" texture (mean): 9.71 39.28\n",
" perimeter (mean): 43.79 188.5\n",
" area (mean): 143.5 2501.0\n",
" smoothness (mean): 0.053 0.163\n",
" compactness (mean): 0.019 0.345\n",
" concavity (mean): 0.0 0.427\n",
" concave points (mean): 0.0 0.201\n",
" symmetry (mean): 0.106 0.304\n",
" fractal dimension (mean): 0.05 0.097\n",
" radius (standard error): 0.112 2.873\n",
" texture (standard error): 0.36 4.885\n",
" perimeter (standard error): 0.757 21.98\n",
" area (standard error): 6.802 542.2\n",
" smoothness (standard error): 0.002 0.031\n",
" compactness (standard error): 0.002 0.135\n",
" concavity (standard error): 0.0 0.396\n",
" concave points (standard error): 0.0 0.053\n",
" symmetry (standard error): 0.008 0.079\n",
" fractal dimension (standard error): 0.001 0.03\n",
" radius (worst): 7.93 36.04\n",
" texture (worst): 12.02 49.54\n",
" perimeter (worst): 50.41 251.2\n",
" area (worst): 185.2 4254.0\n",
" smoothness (worst): 0.071 0.223\n",
" compactness (worst): 0.027 1.058\n",
" concavity (worst): 0.0 1.252\n",
" concave points (worst): 0.0 0.291\n",
" symmetry (worst): 0.156 0.664\n",
" fractal dimension (worst): 0.055 0.208\n",
" ===================================== ======= ========\n",
"\n",
" :Missing Attribute Values: None\n",
"\n",
" :Class Distribution: 212 - Malignant, 357 - Benign\n",
"\n",
" :Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian\n",
"\n",
" :Donor: Nick Street\n",
"\n",
" :Date: November, 1995\n",
"\n",
"This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.\n",
"https://goo.gl/U2Uwz2\n",
"\n",
"Features are computed from a digitized image of a fine needle\n",
"aspirate (FNA) of a breast mass. They describe\n",
"characteristics of the cell nuclei present in the image.\n",
"A few of the images can be found at\n",
"http://www.cs.wisc.edu/~street/images/\n",
"\n",
"Separating plane described above was obtained using\n",
"Multisurface Method-Tree (MSM-T) [K. P. Bennett, \"Decision Tree\n",
"Construction Via Linear Programming.\" Proceedings of the 4th\n",
"Midwest Artificial Intelligence and Cognitive Science Society,\n",
"pp. 97-101, 1992], a classification method which uses linear\n",
"programming to construct a decision tree. Relevant features\n",
"were selected using an exhaustive search in the space of 1-4\n",
"features and 1-3 separating planes.\n",
"\n",
"The actual linear program used to obtain the separating plane\n",
"in the 3-dimensional space is that described in:\n",
"[K. P. Bennett and O. L. Mangasarian: \"Robust Linear\n",
"Programming Discrimination of Two Linearly Inseparable Sets\",\n",
"Optimization Methods and Software 1, 1992, 23-34].\n",
"\n",
"This database is also available through the UW CS ftp server:\n",
"\n",
"ftp ftp.cs.wisc.edu\n",
"cd math-prog/cpo-dataset/machine-learn/WDBC/\n",
"\n",
"References\n",
"----------\n",
" - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction \n",
" for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on \n",
" Electronic Imaging: Science and Technology, volume 1905, pages 861-870, \n",
" San Jose, CA, 1993. \n",
" - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and \n",
" prognosis via linear programming. Operations Research, 43(4), pages 570-577, \n",
" July-August 1995.\n",
" - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques\n",
" to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) \n",
" 163-171.\n",
"\n"
]
}
],
"source": [
"print(cancer['DESCR'])"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])\n",
"#(['DESCR', 'data', 'feature_names', 'target_names', 'target'])"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Libraries"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import pandas as pd\n",
"import numpy as np\n",
"import seaborn as sns\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The Data\n",
"\n",
"Let's work with the cancer data set again since it had so many features."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn.datasets import load_breast_cancer"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cancer = load_breast_cancer()"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"dict_keys(['DESCR', 'data', 'feature_names', 'target_names', 'target'])"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cancer.keys()"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Breast Cancer Wisconsin (Diagnostic) Database\n",
"\n",
"Notes\n",
"-----\n",
"Data Set Characteristics:\n",
" :Number of Instances: 569\n",
"\n",
" :Number of Attributes: 30 numeric, predictive attributes and the class\n",
"\n",
" :Attribute Information:\n",
" - radius (mean of distances from center to points on the perimeter)\n",
" - texture (standard deviation of gray-scale values)\n",
" - perimeter\n",
" - area\n",
" - smoothness (local variation in radius lengths)\n",
" - compactness (perimeter^2 / area - 1.0)\n",
" - concavity (severity of concave portions of the contour)\n",
" - concave points (number of concave portions of the contour)\n",
" - symmetry \n",
" - fractal dimension (\"coastline approximation\" - 1)\n",
" \n",
" The mean, standard error, and \"worst\" or largest (mean of the three\n",
" largest values) of these features were computed for each image,\n",
" resulting in 30 features. For instance, field 3 is Mean Radius, field\n",
" 13 is Radius SE, field 23 is Worst Radius.\n",
" \n",
" - class:\n",
" - WDBC-Malignant\n",
" - WDBC-Benign\n",
"\n",
" :Summary Statistics:\n",
"\n",
" ===================================== ======= ========\n",
" Min Max\n",
" ===================================== ======= ========\n",
" radius (mean): 6.981 28.11\n",
" texture (mean): 9.71 39.28\n",
" perimeter (mean): 43.79 188.5\n",
" area (mean): 143.5 2501.0\n",
" smoothness (mean): 0.053 0.163\n",
" compactness (mean): 0.019 0.345\n",
" concavity (mean): 0.0 0.427\n",
" concave points (mean): 0.0 0.201\n",
" symmetry (mean): 0.106 0.304\n",
" fractal dimension (mean): 0.05 0.097\n",
" radius (standard error): 0.112 2.873\n",
" texture (standard error): 0.36 4.885\n",
" perimeter (standard error): 0.757 21.98\n",
" area (standard error): 6.802 542.2\n",
" smoothness (standard error): 0.002 0.031\n",
" compactness (standard error): 0.002 0.135\n",
" concavity (standard error): 0.0 0.396\n",
" concave points (standard error): 0.0 0.053\n",
" symmetry (standard error): 0.008 0.079\n",
" fractal dimension (standard error): 0.001 0.03\n",
" radius (worst): 7.93 36.04\n",
" texture (worst): 12.02 49.54\n",
" perimeter (worst): 50.41 251.2\n",
" area (worst): 185.2 4254.0\n",
" smoothness (worst): 0.071 0.223\n",
" compactness (worst): 0.027 1.058\n",
" concavity (worst): 0.0 1.252\n",
" concave points (worst): 0.0 0.291\n",
" symmetry (worst): 0.156 0.664\n",
" fractal dimension (worst): 0.055 0.208\n",
" ===================================== ======= ========\n",
"\n",
" :Missing Attribute Values: None\n",
"\n",
" :Class Distribution: 212 - Malignant, 357 - Benign\n",
"\n",
" :Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian\n",
"\n",
" :Donor: Nick Street\n",
"\n",
" :Date: November, 1995\n",
"\n",
"This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.\n",
"https://goo.gl/U2Uwz2\n",
"\n",
"Features are computed from a digitized image of a fine needle\n",
"aspirate (FNA) of a breast mass. They describe\n",
"characteristics of the cell nuclei present in the image.\n",
"A few of the images can be found at\n",
"http://www.cs.wisc.edu/~street/images/\n",
"\n",
"Separating plane described above was obtained using\n",
"Multisurface Method-Tree (MSM-T) [K. P. Bennett, \"Decision Tree\n",
"Construction Via Linear Programming.\" Proceedings of the 4th\n",
"Midwest Artificial Intelligence and Cognitive Science Society,\n",
"pp. 97-101, 1992], a classification method which uses linear\n",
"programming to construct a decision tree. Relevant features\n",
"were selected using an exhaustive search in the space of 1-4\n",
"features and 1-3 separating planes.\n",
"\n",
"The actual linear program used to obtain the separating plane\n",
"in the 3-dimensional space is that described in:\n",
"[K. P. Bennett and O. L. Mangasarian: \"Robust Linear\n",
"Programming Discrimination of Two Linearly Inseparable Sets\",\n",
"Optimization Methods and Software 1, 1992, 23-34].\n",
"\n",
"This database is also available through the UW CS ftp server:\n",
"\n",
"ftp ftp.cs.wisc.edu\n",
"cd math-prog/cpo-dataset/machine-learn/WDBC/\n",
"\n",
"References\n",
"----------\n",
" - W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction \n",
" for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on \n",
" Electronic Imaging: Science and Technology, volume 1905, pages 861-870, \n",
" San Jose, CA, 1993. \n",
" - O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and \n",
" prognosis via linear programming. Operations Research, 43(4), pages 570-577, \n",
" July-August 1995.\n",
" - W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques\n",
" to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) \n",
" 163-171.\n",
"\n"
]
}
],
"source": [
"print(cancer['DESCR'])"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])\n",
"#(['DESCR', 'data', 'feature_names', 'target_names', 'target'])"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"| \n", " | mean radius | \n", "mean texture | \n", "mean perimeter | \n", "mean area | \n", "mean smoothness | \n", "mean compactness | \n", "mean concavity | \n", "mean concave points | \n", "mean symmetry | \n", "mean fractal dimension | \n", "... | \n", "worst radius | \n", "worst texture | \n", "worst perimeter | \n", "worst area | \n", "worst smoothness | \n", "worst compactness | \n", "worst concavity | \n", "worst concave points | \n", "worst symmetry | \n", "worst fractal dimension | \n", "
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | \n", "17.99 | \n", "10.38 | \n", "122.80 | \n", "1001.0 | \n", "0.11840 | \n", "0.27760 | \n", "0.3001 | \n", "0.14710 | \n", "0.2419 | \n", "0.07871 | \n", "... | \n", "25.38 | \n", "17.33 | \n", "184.60 | \n", "2019.0 | \n", "0.1622 | \n", "0.6656 | \n", "0.7119 | \n", "0.2654 | \n", "0.4601 | \n", "0.11890 | \n", "
| 1 | \n", "20.57 | \n", "17.77 | \n", "132.90 | \n", "1326.0 | \n", "0.08474 | \n", "0.07864 | \n", "0.0869 | \n", "0.07017 | \n", "0.1812 | \n", "0.05667 | \n", "... | \n", "24.99 | \n", "23.41 | \n", "158.80 | \n", "1956.0 | \n", "0.1238 | \n", "0.1866 | \n", "0.2416 | \n", "0.1860 | \n", "0.2750 | \n", "0.08902 | \n", "
| 2 | \n", "19.69 | \n", "21.25 | \n", "130.00 | \n", "1203.0 | \n", "0.10960 | \n", "0.15990 | \n", "0.1974 | \n", "0.12790 | \n", "0.2069 | \n", "0.05999 | \n", "... | \n", "23.57 | \n", "25.53 | \n", "152.50 | \n", "1709.0 | \n", "0.1444 | \n", "0.4245 | \n", "0.4504 | \n", "0.2430 | \n", "0.3613 | \n", "0.08758 | \n", "
| 3 | \n", "11.42 | \n", "20.38 | \n", "77.58 | \n", "386.1 | \n", "0.14250 | \n", "0.28390 | \n", "0.2414 | \n", "0.10520 | \n", "0.2597 | \n", "0.09744 | \n", "... | \n", "14.91 | \n", "26.50 | \n", "98.87 | \n", "567.7 | \n", "0.2098 | \n", "0.8663 | \n", "0.6869 | \n", "0.2575 | \n", "0.6638 | \n", "0.17300 | \n", "
| 4 | \n", "20.29 | \n", "14.34 | \n", "135.10 | \n", "1297.0 | \n", "0.10030 | \n", "0.13280 | \n", "0.1980 | \n", "0.10430 | \n", "0.1809 | \n", "0.05883 | \n", "... | \n", "22.54 | \n", "16.67 | \n", "152.20 | \n", "1575.0 | \n", "0.1374 | \n", "0.2050 | \n", "0.4000 | \n", "0.1625 | \n", "0.2364 | \n", "0.07678 | \n", "
5 rows × 30 columns
\n", "